Seit 2003 prägt Domain-Driven Design – manifestiert durch das sogenannte „Blue Book“ von Eric Evans – unsere Sicht auf Softwareentwicklung und deren Verbindung zu Organisation und Fachlichkeit. Durch leistungsfähige Infrastruktur bei stetig steigender inhaltlicher Komplexität verlagert sich der Fokus von Technik und Hardware hin zur Modellierung und dem logischen Schnitt von Systemen. Eben diesen Schritt setzt das Domain-Driven Design sowohl an den Beginn als auch in den Fokus des Entwurfs.
Aufgeteilt wird das Vorgehen dabei in zwei Teilbereiche: Strategic Design und Tactical Design. Ersteres wird benötigt, um den Problemraum abzugrenzen und in handhabbare und gut voneinander zu trennende Teile aufzuspalten. Das zweite findet Anwendung bei der Übersetzung des Problemraums in konkrete Software im Lösungsraum (Kasten: „Problem- und Lösungsraum“). Für beide Teilbereiche werden Informationen aus Organisation und Fachlichkeit herangezogen: von Geschäftsobjekten über Organisationsstrukturen und Teamzusammensetzungen bis hin zu Prozessen. Es ist die Technik, die sich an diese Gegebenheiten anzupassen und sie zu unterstützen hat, nicht andersherum.
Problem- und Lösungsraum
Der Problemraum beschreibt die Gesamtheit der zu lösenden Themen. Hierunter fallen funktionale und Qualitätsanforderungen sowie Randbedingungen. Formuliert wird der Problemraum von Stakeholdern, also jenen Rollen und Personen, die ein berechtigtes Interesse an den Themen haben. Zusammenfassend kann man sagen, dass sich aus dem Problemraum das Was des Entwurfs ergibt.
Der Lösungsraum umfasst die gestalterischen und technischen Mittel, mit denen die Themen des Problemraums gelöst werden können. Dazu gehören das Design, die Architektur und die Implementierung einer Software, wenn diese die Anforderungen zu erfüllen vermag. Aus dem Lösungsraum ergibt sich das Wie des Entwurfs.
Dem Blue Book von Eric Evans [1] folgten zahlreiche weitere Werke, die das Domain-Driven Design weiterentwickelten und anpassten. Unter anderem das „Red Book“ von Vaughn Vernon [2], das sich auf die praktische Umsetzung konzentriert, und das Werk von Vlad Kononov [3]. Diese Bücher veranschaulichen, wie für die Softwareentwicklung nützliche Patterns im Kontext des Tactical Designs identifiziert und in Software gegossen werden.

Systeme modernisieren statt nur migrieren
Power-Workshops zu Modernisierung & Service-Architektur (22. - 26. Juni 2026, München)
Entities und Value Objects
Beispiele für solche Patterns sind die Unterscheidung von Entities und Value Objects. Entities beziehen sich auf Geschäftsobjekte, die einen eindeutigen Identifikator besitzen und gleichzeitig einen Lebenszyklus durchlaufen. Diese Objekte verändern sich möglicherweise im Laufe ihres Lebens, der Identifikator dagegen bleibt immer gleich. Value Objects bilden Geschäftsobjekte ab, deren Identifikator durch ihre Identität abgebildet wird, sprich, durch die Gesamtheit ihrer Eigenschaften. Sie sind unveränderlich und besitzen keinen Lebenszyklus. Als Beispiel soll uns hier das klassische Geschäftsobjekt „Kunde“ dienen. Dieser entspricht einer Entity, hat meist eine eindeutig identifizierende Kundennummer und durchläuft einen Lebenszyklus.
Innerhalb dieses Lebenszyklus kann die Adresse oder auch der Name gewechselt werden (zum Beispiel durch einen Umzug oder Heirat). Die Adresse selbst stellt ein Value Object dar. Sie wird identifiziert durch die Gesamtheit ihrer Eigenschaften (Straße, Hausnummer, Stadt, Postleitzahl). Sie verändert sich nicht, sondern wird nur im Ganzen ausgetauscht.
Strukturen aus Geschäftsobjekten
Die Grundidee, Strukturen für Software aus den Geschäftsobjekten abzuleiten, die sie abbilden sollen, ist kein Novum des Domain-Driven Designs. Sowohl in der klassischen, objektorientierten als auch in der funktionalen Programmierung finden sich ähnliche Ansätze. In der objektorientierten Programmierung wird dies durch Klassen und Objekte umgesetzt, die die Geschäftsobjekte und deren Verhalten abbilden. Diese inhaltliche Nähe findet sich in der oben aufgeführten Literatur wieder, in der mit objektorientierten Beispielen gearbeitet wird. In der funktionalen Programmierung hingegen werden algebraische Strukturen gesucht, die der Fachlichkeit zugrunde liegen und deren Eigenschaften der Software zugutekommen. Die Kombination aus beidem möchte ich anhand eines Beispiels verdeutlichen.
Geschäftsobjekte
Als Beispiel beschäftigen wir uns mit der Software für die Zugangskontrolle in einem großen, kommerziellen Gebäudekomplex, einem Bürogebäude. In einem ersten Schritt müssen wir auf Basis von Stakeholder-Befragungen, des Studiums von Dokumentationen sowie bereits bestehender Systeme für die Zugangskontrolle relevante Geschäftsobjekte identifizieren. In jedem Umfeld (sei es ein Unternehmen oder eine Organisation) gibt es Unmengen an Geschäftsobjekten und für jedes eine Vielzahl von Eigenschaften. Im folgenden Schritt interessieren wir uns jedoch lediglich für Geschäftsobjekte, die im Kontext der Zugangskontrolle eine Rolle spielen, und bei diesen nur für jene Eigenschaften, die wiederum in unseren fachlichen Regeln eine Rolle spielen. Im Folgenden beschreiben wir die Geschäftsobjekte für unser Beispiel (Kasten: „Benennung von Geschäftsobjekten).
Benennung von Geschäftsobjekten
Das Domain-Driven Design führt den Begriff der Ubiquitous Language ein. Es handelt sich hierbei um eine gemeinsames Sprachverständnis aller Stakeholder eines Systems, technisch wie fachlich. Die Benennung der Geschäftsobjekte ist ein zentraler Bestandteil der Ubiquitous Language und kann nur im Einklang mit allen Stakeholdern erfolgen. Erst wenn sich die Fachbegriffe der Domänenexperten genauso auch im Entwurf und im Code wiederfinden, ist es möglich, ein alle Rollen übergreifendes Verständnis für sie zu entwickeln.
Gebäudekomplex, Gebäude, Etage, Raum
Alle aufgeführten Geschäftsobjekte beschreiben Bereiche innerhalb des Gebäudekomplexes bzw. den Gebäudekomplex selbst. Sie können in einer Art Hierarchie angeordnet werden. Für die Zugangskontrolle sind die individuellen Eigenschaften der Geschäftsobjekte – etwa die Adresse eines Gebäudes oder die Etagennummer – lediglich als Identifikatoren relevant. Daher können sie aus dieser Perspektive als Value Objects eines Typs Zugangsbereich abgebildet werden.
Mitarbeiter, Besucher
Diese Geschäftsobjekte beschreiben Personen, die Zugang zum Gebäude haben. Sie besitzen jeweils einen eindeutigen Identifikator (Mitarbeiter-ID, Besucherausweis) und eine Definition ihrer Zugangsberechtigung. Sie durchlaufen einen Lebenszyklus (Mitarbeiter können das Unternehmen verlassen, Besucher können nur temporär im Gebäude sein), daher lassen sie sich als Entities eines Typs abbilden: Person.
Zugang
Dieses Geschäftsobjekt beschreibt die Berechtigung, die eine Person benötigt, um einen bestimmten Zugangsbereich zu betreten. Es handelt sich hierbei um eine Referenz auf einen oder mehrere Zugangsbereiche, die mit einer gewissen Semantik versehen ist. Die Referenz befindet sich im Besitz einer Person. Dementsprechend lässt sich der Zugang als Value Object des Typs Zugangsberechtigung abbilden.
Potenzial der Geschäftsobjekte
Bevor wir uns auf die Suche nach möglichen algebraischen Strukturen machen, ist es sinnvoll, die Komplexität und das Potenzial der Geschäftsobjekte und ihrer resultierenden Typen einzuschätzen. Leitfragen hierbei sind:
-
Wie viel meiner fachlichen Komplexität bezieht sich auf das Geschäftsobjekt und dessen Typ?
-
Ergibt das Geschäftsobjekt in einer kombinierten Struktur (sprich, mehrere Instanzen des Geschäftsobjektes zusammen) Sinn?
-
Welches Potenzial ergibt sich aus der Kombination mehrerer Instanzen des Geschäftsobjekts?
Für die Typen der oben genannten Geschäftsobjekte treffen wir nun eine Einschätzung.
Zugangsbereich
Die fachliche Komplexität, die ein Zugangsbereich mit sich bringt, ist gering. Es handelt sich um einen logischen Baustein, der die statische Struktur einer Immobilie abbildet. Eine Kombination von Zugangsbereichen ist definitiv sinnvoll, da diese zueinander in einer hierarchischen Beziehung stehen (zum Beispiel ist eine Etage Teil eines Gebäudes, das wiederum Teil eines Gebäudekomplexes sein kann). Aus der Kombination von Zugangsbereichen ergibt sich eine deutliche Vereinfachung der Formulierung von Zugangsberechtigungen. Anstatt einer Person Zugangsberechtigungen für jeden einzelnen Zugangsbereich unterhalb eines großen Bereiches zu geben, reicht die Vergabe einer einzigen Berechtigung aus. Damit wird auch die übliche Ausdrucksweise und das Verständnis der Stakeholder ausgedrückt.
Person
Die fachliche Komplexität, die eine Person darstellt, ist ebenfalls gering. Für die Zugangskontrolle sind alle Eigenschaften von Personen irrelevant, außer deren Identifikatoren und konkreten Berechtigungen. Auch eine Kombination von Personen ergibt keinen Sinn, da Personen, die sich in der Regel individuell bewegen können, für die Zugangskontrolle nicht sinnvoll in Gruppen zusammengefasst werden können.
Zugangsberechtigung
Die fachliche Komplexität der Zugangsberechtigungen ist hoch, hier steckt der Kern dessen, womit sich die Zugangskontrolle beschäftigt. Die Kombination von Zugangsberechtigungen ermöglicht es, die individuellen Berechtigungen einzelner Personen abzubilden und diese flexibel anzupassen. Das Potenzial hierbei ist sehr groß, da die fachlichen Regeln in fast allen Fällen einer Komposition von Zugangsberechtigungen entsprechen. Zum Beispiel benötigt eine Person, die ein Büro im zweiten Stockwerk bezieht, Zugangsberechtigungen für den Eingangsbereich des Gebäudes sowie für die zweite Etage.
Algebraische Strukturen
Jetzt, da wir eine Einschätzung für die Typen der Geschäftsobjekte vorgenommen haben, können wir nach algebraischen Strukturen bei Zugangsbereichen und Zugangsberechtigungen suchen. Algebraische Strukturen entstammen der Mathematik und definieren sich anhand einer Menge von Elementen (in unserem Fall der Typ), einer kombinierenden Operation auf dieser Menge und Eigenschaften der Operation. Es gibt viele verschiedene algebraische Strukturen mit unterschiedlicher Komplexität; es ist sinnvoll hier mit den grundlegenden Strukturen zu beginnen und sich schrittweise zu den komplexeren vorzuarbeiten. Je komplexer die Struktur ist, die wir für einen Typ identifizieren, desto mehr Gesetzmäßigkeiten gelten für ihn.
Magma
Ein Magma ist eine Menge von Elementen, auf denen eine Operation definiert ist, die für jedes Paar von Elementen ein drittes Element derselben Menge liefert. Diese Struktur ist jedoch nicht notwendigerweise assoziativ oder kommutativ. Jedes sinnvoll kombinierbare Geschäftsobjekt bildet zusammen mit seiner Kombinationslogik ein Magma. Ein gut nachvollziehbares Beispiel für ein Magma ist die Division als Operation auf der Menge der positiven Zahlen:
Magma (M, *) mit *:M×M→M
Halbgruppe
Die Halbgruppe baut auf den Eigenschaften des Magmas auf. Für die Operation gilt allerdings das Assoziativgesetz. Bei einer mehrfachen Ausführung der Operation hintereinander spielt die Reihenfolge, in der die Ergebnisse kombiniert werden, demnach keine Rolle. Ein Beispiel für eine Halbgruppe ist die Menge der natürlichen Zahlen mit der Addition als Operation:
Halbgruppe (M,*) mit *:M×M→M; ∀a,b,c∈M:a*(b*c)=(a*b)*c
Monoid
Der Monoid baut auf den Eigenschaften der Halbgruppe auf. Für die Operation gilt nicht nur das Assoziativgesetz, zusätzlich wird ein sogenanntes neutrales Element benötigt. Wird dieses als einer der Parameter der Operation verwendet, entspricht das Ergebnis immer exakt dem anderen Parameter. Ein Beispiel für ein Monoid ist die Multiplikation der natürlichen Zahlen und der 1 als neutralem Element.
Monoid (M,*) mit *:M×M→M; ∀a,b,c∈M:a*(b*c)=(a*b)*c
und dem neutralen Element n mit ∀a∈M:a*n=a
Gruppe
Die Gruppe ist die nächstkomplexere Struktur auf Basis des Monoiden und erweitert diesen um ein Inverses. Das Inverse ist ein Element, das bei der Anwendung der Operation auf ein anderes Element das neutrale Element als Ergebnis zurückliefert. Es muss sich dabei nicht um genau ein Element handeln, es muss lediglich eines für jedes andere Element der Menge existieren. Ein Beispiel für eine Gruppe ist die Menge der ganzen Zahlen mit der Addition als Operation, wobei 0 das neutrale Element und -x das Inverse von x ist:
Gruppe (M,*) mit *:M×M→M; ∀a,b,c∈M:a*(b*c)=(a*b)*c
und dem neutralen Element n mit ∀a∈M:a*n=a
und dem Inversen ∀a∈M:a*a-1=n
| Algebraische Struktur | Assoziativität | Neutrales Element | Inverses |
|---|---|---|---|
| Magma | X | X | X |
| Halbgruppe | √ | X | X |
| Monoid | √ | √ | X |
| Gruppe | √ | √ | √ |
Tabelle 1: Vergleich verschiedener algebraischer Strukturen
Algebraische Strukturen identifizieren
Nehmen wir uns also die Typen der Geschäftsobjekte mit dem größten Potenzial vor und schauen, ob und welche algebraische Struktur wir hier identifizieren können.
Zugangsbereich:
-
Elemente: Die Menge besteht aus allen Zugangsbereichen, die auf Gebäudekomplexen definiert werden können.
-
Operation: Eine Operation, um aus zwei Zugangsbereichen einen neuen zu bilden, ist die hierarchische Unterordnung. Mit dieser können zum Beispiel zwei Etagen zu einem Gebäude zusammengefasst werden. Bei Zugangsbereichen ist es außerdem möglich, mehr als nur zwei Elemente zu einem neuen Element zu kombinieren, zum Beispiel bei einem drei- oder vierstöckigen Gebäude.
-
Assoziativität: Die hierarchische Unterordnung von Zugangsbereichen ist nicht assoziativ. Es macht durchaus einen Unterschied, ob Etagen erst zu einem Gebäude und dann zu einem Gebäudekomplex zusammengefasst werden oder ob sie erst zu einem Gebäudekomplex und dieser dann einem Gebäude zugeordnet wird.
-
Neutrales Element: Aus der Fachlichkeit ergibt sich kein sinnvolles neutrales Element in der Menge der Zugangsbereiche. Es gibt keinen Zugangsbereich, der bei der hierarchischen Unterordnung keine Veränderung bewirken würde.
-
Inverses: Da es kein sinnvolles neutrales Element in der Menge der Zugangsbereiche gibt, kann auch kein Inverses definiert werden.
-
Fazit: Den Zugangsbereichen liegt nur eine sehr rudimentäre algebraische Struktur zugrunde. Durch die Kombinationsfähigkeit bilden sie ein Magma.
Zugangsberechtigung:
-
Elemente: Die Menge besteht aus allen Zugangsberechtigungen, die zwischen Gebäudekomplexen und Personen vergeben werden können.
-
Operation: Es gibt mehrere fachlich relevante Operationen, die auf Zugangsberechtigungen angewendet werden können. Die offensichtlichste ist die Vereinigung. Diese wird üblicherweise angewendet, wenn in der Beschreibung der Berechtigungen das Wort „und“ verwendet wird. Zum Beispiel der Zugang zum Eingangsbereich eines Gebäudes und zur zweiten Etage. Eine weitere Operation ist die Differenz. Diese wird verwendet, wenn in der Beschreibung das Wort „außer“ verwendet wird. Zum Beispiel der Zugang zur zweiten Etage außer dem Aktenlagerraum.
-
Assoziativität: Die Vereinigung von Zugangsberechtigungen ist assoziativ. Es spielt keine Rolle, in welcher Reihenfolge die Berechtigungen kombiniert werden, das Ergebnis bleibt immer gleich. Die Differenz ist jedoch nicht assoziativ, da die Reihenfolge der Operationen das Ergebnis beeinflusst.
-
Neutrales Element: Das neutrale Element für die Vereinigung ist die leere Zugangsberechtigung, da sie bei der Vereinigung keine Veränderung bewirkt. Sie entspricht dem fachlichen Umstand, dass eine Person schlicht keine Zugangsberechtigung hat. Für die Differenz gibt es kein neutrales Element.
-
Inverses: Jede Zugangsberechtigung erweitert die Menge der Zugangsbereiche, die eine Person betreten darf. Demnach ist es nicht möglich, Zugangsberechtigungen zu definieren, die der Person Zugang zu Bereichen entzieht. Es kann also kein Inverses definiert werden.
-
Fazit: Die Zugangsberechtigungen bilden mit der Vereinigung einen Monoiden. Mit der Differenz bilden sie jedoch lediglich ein Magma, da hier weder Assoziativität noch ein neutrales Element gegeben sind.
Algebraische Datentypen
Um die Erkenntnisse, die wir bis jetzt zu den Geschäftsobjekten gewonnen haben, in der Software abbilden zu können, bieten sich algebraische Datentypen an. Hierbei unterscheidet man zwei verschiedene Typen: Produkte und Summen (Kasten: „Produkt und Summe“). Produkte sind Datentypen, deren Wert sich aus anderen Datentypen zusammensetzt. Summen sind Datentypen, deren Wert sich aus einer Auswahl von Ausprägungen ergibt. Es gibt keine feste Zuordnung zwischen Entities und Value Objects auf der einen und Produkten und Summen auf der anderen Seite (Abb. 1).
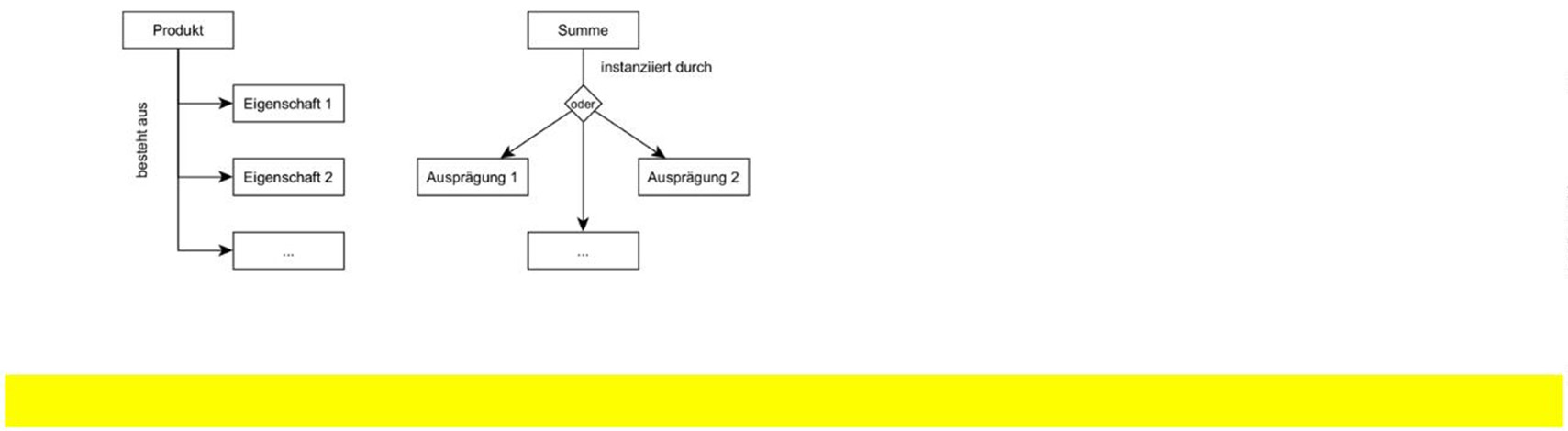
Produkt und Summe
Die Bezeichnung der algebraischen Datentypen Produkt und Summe ergibt sich aus der Rechenvorschrift, mit der die Menge aller Werte bestimmt werden kann. Die Menge aller möglichen Werte eines Produkttyps ergibt sich aus der Multiplikation der Menge aller Werte der einzelnen Eigenschaften. Die Menge aller möglichen Werte eines Summentyps ergibt sich aus der Addition aller möglichen Werte der einzelnen Ausprägungen.
Algebraische Datentypen definieren
Jene Geschäftsobjekte, denen wir algebraische Strukturen zuweisen konnten, lassen sich besonders gut durch Produkte abbilden (Abb. 2). Dabei werden einzelne Ausprägungen genutzt, um die rekursive Vereinigung oder Differenz darzustellen. In funktionalen Programmiersprachen werden algebraische Datentypen meist vom Typsystem direkt unterstützt. Objektorientierte Sprachen arbeiten hauptsächlich mit Produkten, es gibt jedoch auch Möglichkeiten, um Summen abzubilden (zum Beispiel per Sealed Classes in Java).
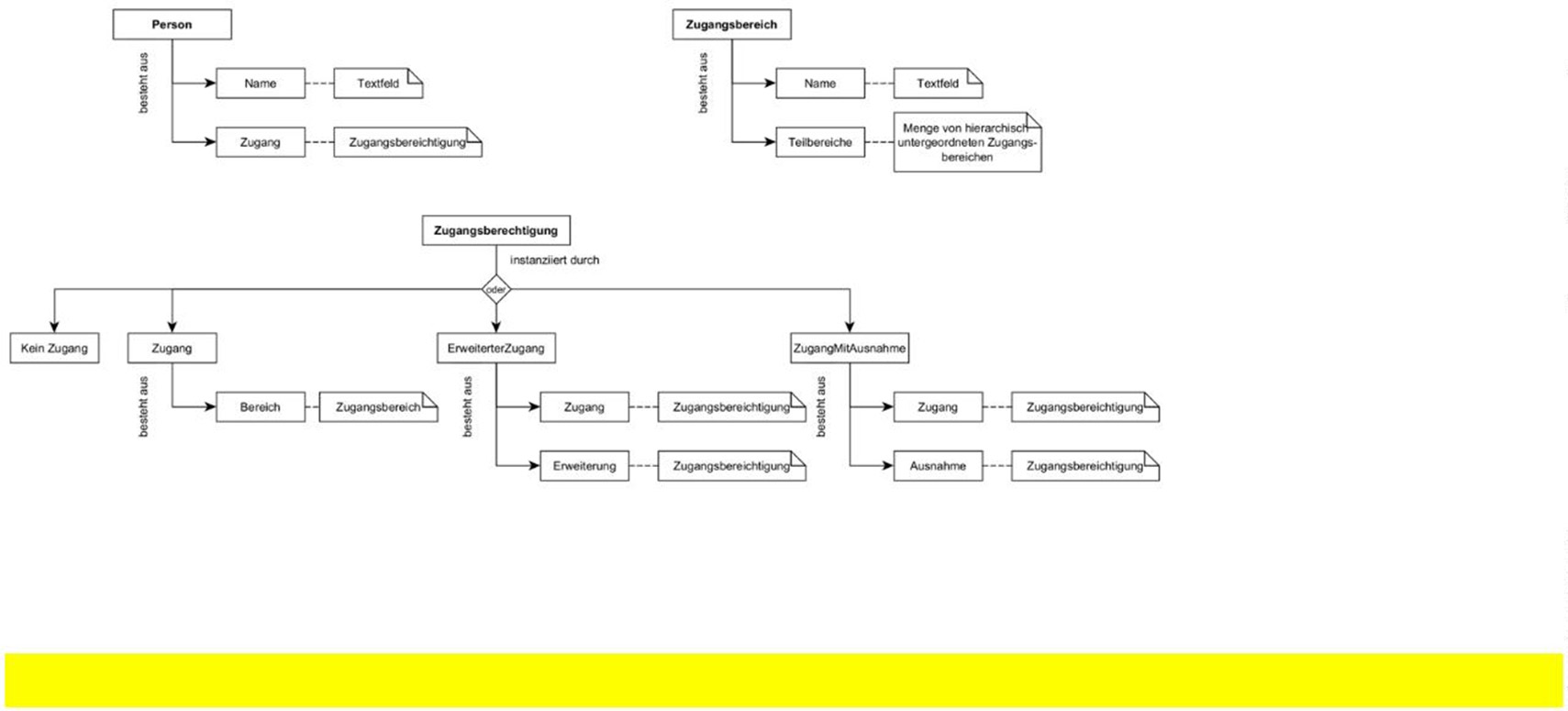
Beispiele
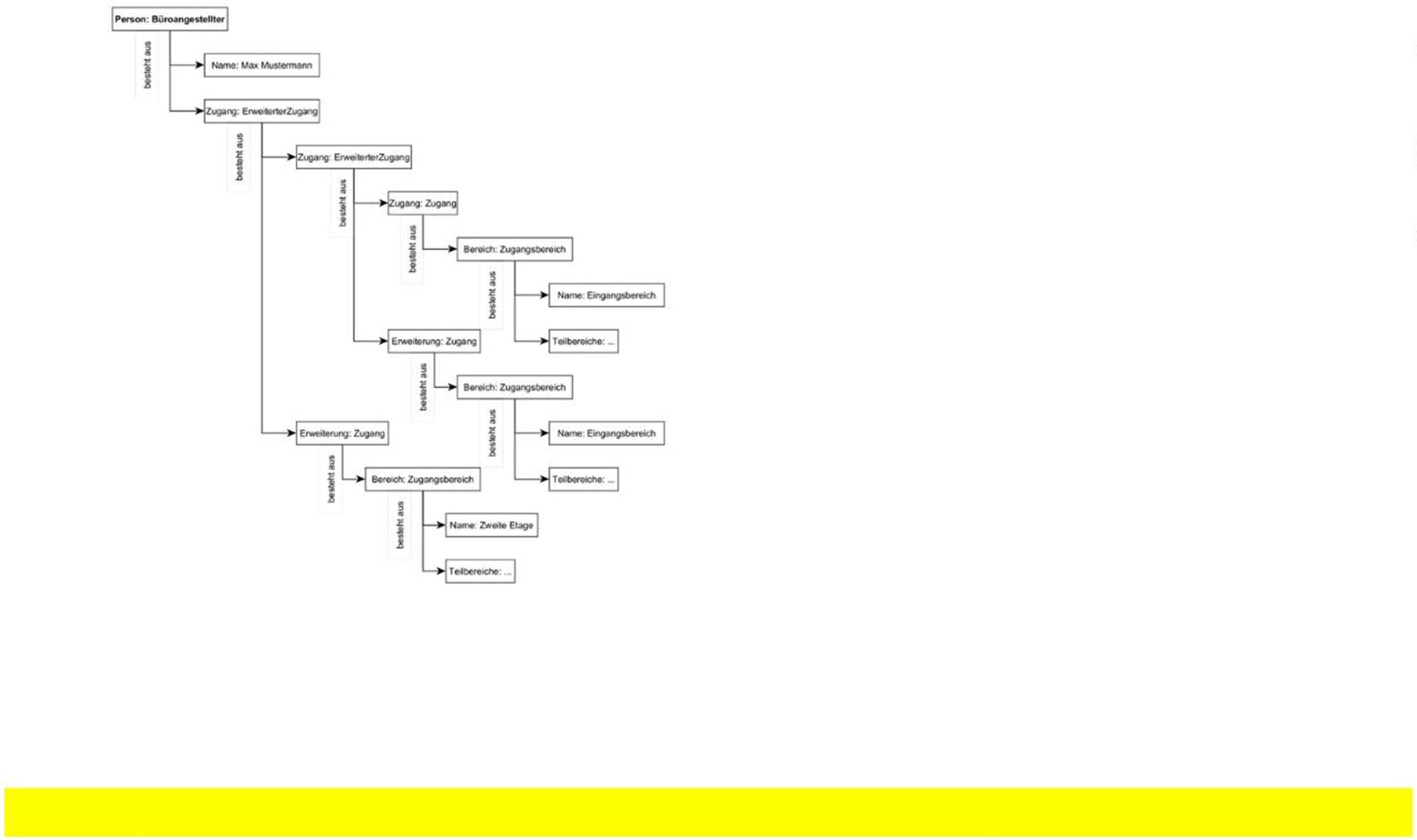
Die beiden Beispiele für Personen mit Zugangsberechtigungen in Abbildung 3 und 4 verdeutlichen, wie fachliche Regeln zur Zugangskontrolle in der Struktur der Datenobjekte abgebildet werden. Die Struktur allein ermöglicht den Rückschluss auf fachliche Regeln, ohne entsprechende Algorithmen oder Programmlogik zur Auswertung zu kennen. Die erste Person stellt einen Büroangestellten dar. Dieser hat Zugang zum Eingangsbereich des Gebäudes, dessen Tiefgarage sowie zur zweiten Etage, auf der sich sein Büro befindet (Abb. 3). Die zweite Person stellt einen Hausmeister dar. Dieser hat Zugang zum gesamten Gebäude, mit Ausnahme eines sensiblen Aktenlagerraumes (Abb. 4).
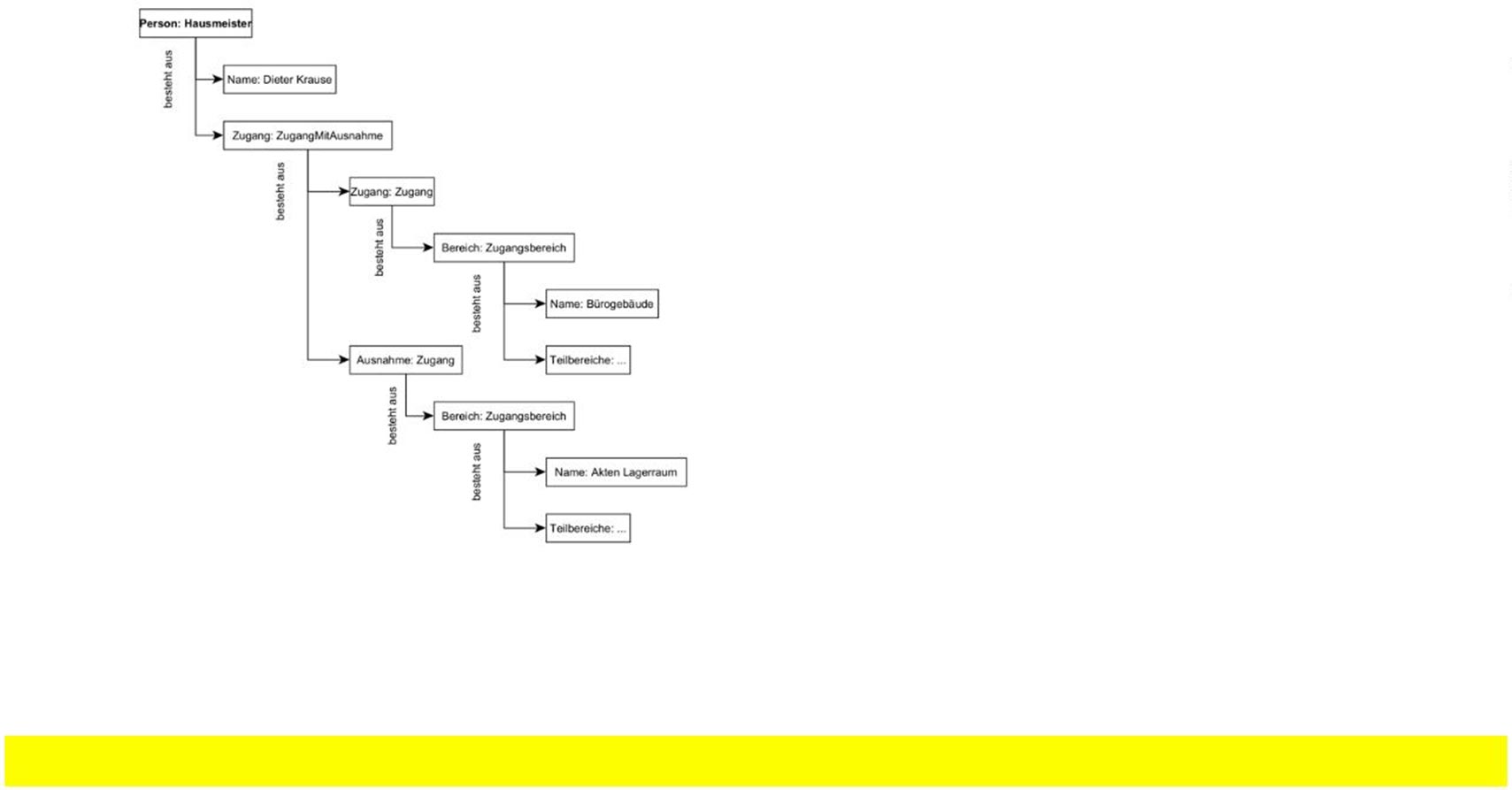
Fazit
Wir haben ein Modell entworfen, das die Fachlichkeit auf explizite Weise darstellt. Die Analyse auf Basis der algebraischen Strukturen ist dabei nicht nur für Entwickler, sondern auch für Fachexperten aufschlussreich und gewährt eine neue Perspektive und Einblicke in die Domäne. Auch wenn die Menge der Ausprägungen eines Produktes fest ist, so lässt sie sich doch im Verlauf der Entwicklung und des Betriebs durch Entwickler einfach erweitern, was die Flexibilität der Software gegenüber fachlichen Änderungen gewährleistet.
Die Rekursion innerhalb der Produkte ermöglicht den Aufbau nahezu beliebig komplexer Instanzen, ohne zusätzliche fachliche Regeln oder ein Aufblähen der Implementierung zu verursachen. Diese Eigenschaft resultiert aus den identifizierten Kombinatoren (Vereinigung, Differenz usw., Kasten: „Kombinatoren“) und lässt sich als fachliche Skalierbarkeit beschreiben.
Kombinatoren
Ein Kombinator beschreibt in der Softwareentwicklung eine in sich geschlossene Funktion. Diese benötigt nur die ihr übergebenen Parameter und greift sonst auf keine Konstanten oder Variablen ihrer Umwelt zu. Kombinatoren im Lösungsraum sind das Gegenstück zu jenen Funktionen, mit denen im Problemraum algebraische Strukturen gebildet werden.
Links & Literatur
[1] Evans, Eric: „Domain-driven design: Tackling Complexity in the Heart of Software“; Addison-Wesley Professional, 2004
[2] Vernon, Vaughn: „Implementing domain-driven design“; Pearson Education, 2013
[3] Khononov, Vlad: „Learning Domain-Driven design: Aligning Software Architecture and Business Strategy“; O’Reilly Media, 2021




